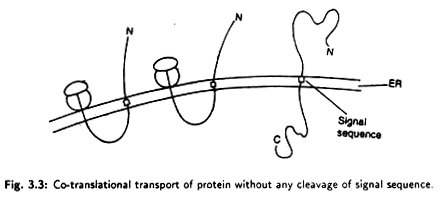
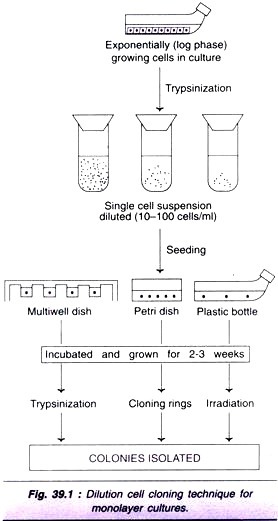
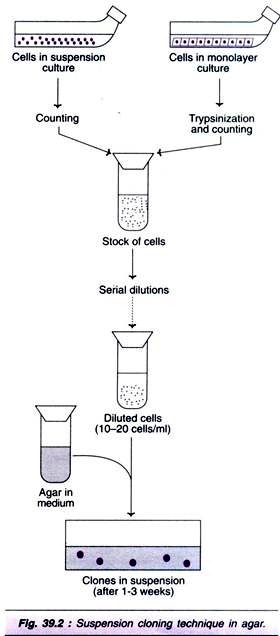
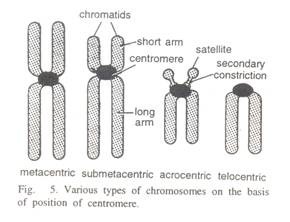
ADVERTISEMENTS:
Any measure of species diversity, by itself, does not convey much information; we appreciate its significance only when we compare with any other measure.
Measures of species diversity can be divided into three categories (Magurran, 1988).
These are:
ADVERTISEMENTS:
(i) Species richness indices,
(ii) Species abundance models, and
(iii) Species proportional abundance based indices
Species Richness Indices:
ADVERTISEMENTS:
Species richness, as measure of diversity, has been used by ecologists. Species density or the number of species per m2 is most commonly used to measure species richness. However, species richness increases with sample size. The smallest sample size may be 1 km^ and the largest may be the entire region or country.
Rarefaction:
As the sample sizes are always unequal, Sanders technique called Rarefaction is used to cope with this difficulty.
Sanders’s formula, as modified by Hurlbert (1971) is as follows:
The simplest approach is to take the number of individuals in the smallest sample as the standardized sample size.
This may be explained with the help of the following example:
If in one catch of fish we obtain 9 species with 23 individuals, and in another catch from the same area made for the same duration we obtained only 13 individuals belonging to 6 species, Hurlberts’ formula may be used to find out the number of species we would have expected in the first catch if it too had only 13 individuals. Thus, expected number of species for the first catch x is 6.6 species (Table 7.4).
Menhinick’s Index (I Mn):
This index is based on the ratio of number of species (S) and the square root of the total number of individuals (N).
ADVERTISEMENTS:
IMn=S/√N or DMn = S/√N
It is claimed that this index may be used to compare samples of different sizes and that the effect of the number of individuals is reduced. However, some authors have shown that this index is not independent of sample size.
Using the data given in Table 7.4, the value of IMn for catch x and catch y will be 1.88 and 1.66 respectively.
Margalefs index (IMg):
ADVERTISEMENTS:
This index also relates the number of species to the number of individuals.
IMg = S – 1/loge N or DMg= (S – 1 )/ln N
The index is influenced by sample size. However, some authors have demonstrated that both this and Manhinick’s index are insensitive to changes in community structure.
Using the data given in Table 7.4, the value of for sample x and sample y will be 2.55 and 1.95 respectively.
ADVERTISEMENTS:
Species Abundance Models:
No community has species of equal abundance. Some species are very abundant, others may have medium abundance and still others may be rare or represented by only a few individuals. This observation led to the development of species abundance models.
Species diversity data is frequently described by one or more patterns of distribution (Piclou, 1975), diversity is usually examined in relation to the following four models:
(a) The geometric series
(b) The log normal distribution
(c) The logarithmic series
ADVERTISEMENTS:
(d) The broken stick model (the random niche boundary hypothesis)
When plotted on a rank abundance graph, the four models represent a progression ranging from the geometric series where a few species are dominant with the remaining fairly uncommon, through the log series and log normal distributions where species of intermediate abundance become more common and ending in the conditions represented by the broken stick model in which species are equally abundant as may be hardly observed.
Species Proportional Abundance Based Indices:
These indices provide an alternative approach to the measurement of diversity. These indices are called heterogeneity indices (Peet 1974) as they take both species richness and evenness into consideration. South wood (1978) called them nonparametric indices in view of the fact that no assumptions are made about the shape of the underlying species abundance distribution. The following indices are used.
Simpson’s Index:
This index relates the contribution made by each species to the total number of individuals present.
ADVERTISEMENTS:
ADVERTISEMENTS:
I = Σ pi2
Where pi is the proportion of individuals in the ith species. The equation given by Wilhm (1967) is the following:
I = Σ (ni(ni-1)/N(N-1)
Where pi = the number of individuals in the ith species and N= the total number of individuals. The values of Simpson’s index range from zero to 1 (unity) and are inversely proportional to the wealth of species (As I increases, diversity decreases). Pielou (1969) has given the following form of equation.
I =1- Σ (ni(ni-1)/N(N-1)
Therefore, index is usually expressed as 1 – I or l/I. The reciprocal form of Simpson’s index ensures that the value of the index increases with diversity.
Shannon Index:
The index independently derived by Shannon and Wiener from the application of information theory is known as the Sharmon index of diversity. It is sometimes incorrectly referred to as the Shannon – weaver index (Krebs, 1985).
The index assumes that:
(a) All species are represented in the sample, and
(b) Individuals are randomly sampled from an ‘indefinitely large’ population (Pielou, 1975).
It is calculated from the equation:
H’ =- Σ pi In pi
Where pi is the proportion of individuals found in the ith species. It is estimated as (ni/N). N is total number of individuals in S species. The value of Shannon index usually varies between 1.5 and 3.5 and rarely exceeds 4.5. The value of H’ is related to species richness but is also influenced by the underlying species abundance distribution. May (1975) has shown that if the underlying distribution is log normal, 10 species will be required to give a value of H’ < 5.0. Log2 is often used to calculate Shannon index. Usually the index is obtained from the series.
H’ = -Σpi In pi – S-1/N+1-Σpi-1 /12N2 + Σ(pi-1 –pi-2)/12N3