Essay on Health Statistics | Branches | Statistics

Here is a compilation of essays on ‘Health Statistics’ for class 11 and 12. Find paragraphs, long and short essays on ‘Health Statistics’ especially written for school and college students.

Essay on Health Statistics

Essay Contents:

1. Essay on the Meaning and Sources of Health Statistics
2. Essay on Graphical & Diagrammatic Representation of Statistical Data 
3. Essay on the Measures of Central Tendency
4. Essay on the Measures of Dispersion
5. Essay on the Measures of Relative Variation
6. Essay on Normal Distribution
7. Essay on Correlation and Regression
8. Essay on Sample Variation & Tests of Significance
9. Essay on Sampling and Its Types

---

ADVERTISEMENTS:

1. Essay on the Meaning and Sources of Health Statistics:

Branch of Statistics deals with methodology of collection, compilation and interpretation of numerical facts concerned with the health, ill-health, and disease variables of human population, e.g. births, deaths, disease pattern, science load, analysis of factors related to diseases, com­pliance and non-compliance of health programme.

Use of Health Information:

1. To estimate the health status of the people and quantitative analysis of health problem and medical and health care needs.

2. To assess the health services as per objec­tives, effectiveness and efficiency

3. For the research purposes into problems of health and diseases.

4. For planning, administration and effective management of health services and pro­grammes.

5. To assess degree of satisfaction by benefici­aries.

6. For the comparison of National and Inter­national Health.

Sources of Health Statistics:

A. For Population:

1. Census reports.

2. Population surveys.

B. For Births:

1. Registers of births.

2. Records of churches.

C. For Deaths:

1. Registers of deaths

2. Registers at the burial and cremation grounds

3. Postmortem records.

D. For Morbidities:

1. Hospital records.

2. Records from private practitioners and dispensaries.

3. Records from health and family welfare centres.

4. Notified disease records.

5. Disease registers.

6. Epidemiological surveillance.

7. Sickness records from Armed Forces.

8. National Sample Surveys Records.

E. For Environmental Health:

1. Environmental Health Data.

2. Population Sample Survey.

F. For Health Manpower/Health Services:

1. Hospital Administration Record.

2. Health Services Administration Record.

---

2. Essay on Graphical & Diagrammatic Representation of Statistical Data:

Uses:

1. Summarisation and reduction of the ob­server is raw data and to depict the essential features embodied in the mass of data.

2. Conclusion can be drawn by seeing the diagram.

3. It exposes hidden relationship of data.

4. They have a general appeal which is able to make an impression at a glance.

Note:

Diagrams prove nothing but bring out stand­ing features readily to the eye, they are, therefore, no substitutes for such critical tests as may be applied to the data are valuable in suggesting such tests and in explaining the conclusion founded upon them.

Selection of Diagram:

A. To Represent Relative Values or Frequencies of Things or Events:

(I) Qualitative Characters:

(i) Bar diagram

(ii) Pie diagram

(II) (i) Histogram

(ii) Frequency Polygon

(iii) Ogive

(III) Quantitative characters (discrete)

B. To Representative Trends of Events or Things in Time and Age:

(i) Line Diagram

(ii) Ratio Chart

C. To Show Geographic Distribution of Things or Events:

(i) Spot map

(ii) Shaded map

D. To Facilitate Computation:

(i) Ogive

Graphic & Diagrammatic Presentation of Data:

1. Line Diagram:

This is simplest type of diagram to study the changes of values of variables with passage of time Diagram is drawn by time (in days, weeks, months and years) along with horizontal axis and values or quantity with vertical axis.

2. Pie Diagram:

In this diagram a circle is divided into dif­ferent sectors corresponding to the frequencies of variables in the distribution. One sector is rep­resenting in proportion in the form of angle which is derived.

No. of observations in specific gps x 260

Total No. of observations in all the groups.

3. Pictogram:

It is useful to them who cannot understand orthodox charts. Small pictures or symbols are used to present the data.

4. Scatter Diagram:

It shows the relationship between two vari­ables e.g. Height and Weight. Each dot represents the height and weight of one child. No. of dots will be equal to the no. of children. If the dots cluster round a straight line, it shows evidence of a relationship of linear nature.

5. Map Diagram or Spot Map:

These maps are prepared to show geographi­cal .distribution of the frequencies of a character­istics. Using different colours on the map of a country may show two different characteristics. Such as attacks and deaths, in different areas, spot map helps in locating or pin-pointing the index case is an epidemic.

6. Bar Charts (Bar Diagram):

This graph is drawn from the frequency distribution table representing the variable on the horizontal axis and the frequency on the vertical axis. Each part or rectangle corresponds to fre­quencies in a class interval.

(A) Simple Bar Chart:

Bars can be drawn vertical or horizontal which are separated at suitable interval—length base are made by deciding scale.

(B) Multiple Bar Chart or Compound Bar Chart:

Multiple bar charts are drawn by two or more bars grouped together.

(C) Component Bar Chart or Proportional Bar Chart:

Bars are divided into two or more parts in which each part represents a certain proportional to the magnitude of that particular item.

7. Histogram:

When quantitative data are of continuous type they are to be depicted in the form of graph. These rectangles are erected as in case of bar diagram with its width equal to the class interval of the variable on the horizontal axis and the corresponding frequency on the vertical axis as its height.

8. Frequency Polygon:

It depicts frequency distribution of quanti­tative data in the form of a curve. It is made by joining the midpoints of the histogram blocks. It is useful to compare two or more frequency distribution by plotting on the same graph which is not possible by histogram because of overlap­ping of boundaries of the rectangles.

9. Ogive:

When a curve is obtained by plotting the cumulative frequencies against the endpoints of the corresponding class intervals. This curve is known as Ogive. This curve is plotted by taking variable on the axis and cumulative frequency on the y-axis.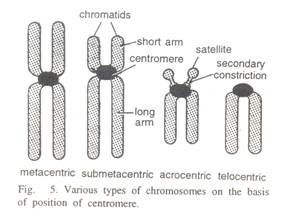

---

3. Essay on the Measures of Central Tendency:

It implies a value in the distribution around which the other values are distributed—it shows an impression of central value.

It includes:

(i) Mean

(ii) Median

(iii) Mode.

(1) Mean:

Arithmatic mean is very commonly used in statistical calculation. Normally it is termed as mean.

Calculation:

(i) Mean =

Sum of all the observations of the data/ No. of observations in the data

∑

—Mean sum of

X₁ is the value of each observation in the data

n is the number of observation in the data

X̅ is symbol of mean

Mean of grouped data

(2) Median:

The median is an average of different kind which does not depend upon the total and number of data.

To obtain the median the data is first arranged in an ascending or descend­ing order of magnitude and then the value of the middle observation is located—which is called the median. There­fore, median is Middle- Most value of data.

1. Arrange the data in Ascending or De­scending order

No. of data/2 = n

Figure at nth place will be median Me­dian = 

(3) Mode:

The mode corresponds to that value of the observation which has highest frequencies. Hence mode is most common value of observation. Main demerit of mode is that exact location is often uncertain and is often not clearly defined, so it is not used very commonly in Biostatistics.

Relationship among Mean,

Median and Mode

Mode = Mean – 3(Mean – Median)

Characteristics of Distribution:

1. Shape of distribution resamples a belt.

2. The curve is symmetrical about the middle point.

3. At the centre of the distribution, which is parked, all the three measures of central tendency—i.e. mean, median and mode— coincide.

4. Maximum number of observations is at the value of the variable corresponding to the mean and the number of observations on both sides of this value gradually decreases and there are few observations at the extreme points.

5. Area covered under two points:

(a) Mean ± 1 S.D. covers 60.3% of the observations

(b) Mean ± 2 S.D. covers 95.4% of the observations

(c) Mean ± 3 S.D. covers 99.7% of the observations.

---

4. Essay on the Measures of Dispersion:

Measures of dispersion depict how observations are scattered from each other or from the mean.

It is also known as measures of variation or measures of deviations.

1. Range:

It is defined as the difference between the highest and lowest figures in given sample.

(i) For ungrouped data

R = (H – L)

R = Range

H = Highest value in sample

L = Lowest value in sample

(ii) For grouped data

R = (Hm – Lm)

Hm = Midpoint of highest category

Lm = Midpoint of lowest category

2. Mean Deviation:

It is the average of the deviations from arithmetic mean and each of the values of the observation in the series of the data.

(i) For Ungrouped Data = 

M.D. = Mean Deviation

X_i = Individual value of the observation

X̅ = Mean

n = No. of observations

(ii) For Grouped Data =

X_i = Middle point of class interval

f_i = Frequency in the class interval

3. Standard Deviation:

In the calculation of mean deviation the sign (-or – -) are taken into consideration. In order to avoid this discrepancy instead of actual values of deviations, the squares of the observations are considered for calculation. This quantity is known as variance. The square root of variance is known as standard deviation. In other words, it is root mean square deviation.

(i) For Ungrouped Data =

---

5. Essay on the Measures of Relative Variation:

1. Coefficient of Variation:

Standard deviation is expressed as a percentage to the mean value and the quantity is known as coefficient of variation. It is expressed in percentage. It is useful to compare the variations of two or more sets of observations which are in different units as well as with marked different units as difference in the size of means whose comparison with standard deviation is not suitable.

2. Skewness:

When frequency distribution or a frequency curve is not symmetrical above the peak it is said to be skewed. In other words, one tail or curve will be longer than the other in a skewed curve.

Skewness can be either to the right or the left of the peak:

Calculation +ve shows skewness right side, -ve shows left side.

---

6. Essay on Normal Distribution:

Normal distribution or normal curve is the most important one in biological observations and most of the biological data follow normal law when considered in large numbers. When frequency polygon is drawn, maximum number of persons corresponds to the centre of the curve, the number of persons gradually decreases along with sides of these points and there is very few observation at the tail end.

Where, y = Frequency corresponding to the variate value x

I₁ Mean value of observations in the population

N = Stand, deviation of the population

R = 3.1459, e = 2.7183

---

7. Essay on Correlation and Regression:

---

8. Essay on Sample Variation & Tests of Significance:

Sampling Variation:

Most of the biological investigations are carried out on samples as it will not be possible to cover the entire population. It is well-known that repeated samples, even from the same population, will not yield the same estimates for any characteristic under observation. Such a difference between sample estimates, even though the samples are from the same population, is known as sampling variations.

Standard Error:

It is the standard deviation of statistical parameter like mean proportion etc. This gives one idea about the dispersion of the above statistical parameter in repeated samples from the same population.

Standard error of a mean gives the standard deviation of all means of several samples taken from the same population. Similarly, standard error of a proportion gives the standard deviation of proportions of several samples of a quantitative data taken from the same population.

where P = Proportion of occurrence of an event

q = (i – p)

n = No. of observations in the sample.

Null Hypothesis:

The first step in the testing of significance of characters to set up a hypothesis appropriate with the problem is called Null Hypothesis—that there was no difference between the effect of two interventions and then proceed to test the hypothesis in quantitative terms.

Level of Significance:

By establishing a null hypothesis it is necessary to fix the magnitude of the risk of making a wrong conclusion of rejecting the null hypothesis that the two groups are from the same population. This quantity is calculated in terms of probability level, denoted by P, and is called as the Level of Significance. It gives the probability of attributing the difference between the sample estimated to sampling variation or chance factor is small.

Method of Testing a Hypothesis:

1. Establish a null hypothesis.

2. Calculate the suitable test of significance using relevant formula for standard error test, test, or F test etc.

3. If sample is smaller than 30 observations use X² test for large sample, more than 30 observations use test, 2 test etc.

4. Determine the degree of freedom.

5. Find out the probability level, P – corresponding to degree of freedom. This can be read out from the tables.

6. Reject the null hypothesis, if P is less than 0.05, otherwise accept it. Therefore, difference between the sample estimates is considered as significant, if P is less than 0.05.

Non-Parametric Test:

Standard error test, t-test or X² test are applicable where variable are distributed normally.

But, sometimes, variables do not confirm to any probability distribution then above tests cannot be applied.

---

9. Essay on Sampling and Its Types:

Sample means a portion or a part of the above population selected in some manner. When some information is required from population it is very unfeasible to collect the information from every individual of universe, we select part of universe which represents the population. The information collected from this sample is representing the information of the Universe.

Applications of Sampling in Community Medicine:

1. To collect advance data from surveys.

2. Evaluation of health status of a population.

3. Investigations of factors influencing health.

4. Studies on environmental hygiene.

5. Studies on the evaluation of health measures.

6. Studies on the administrative aspects of health services.

Types of Sampling:

Several sampling designs are available depending upon the type and natures of the population as well as the object of the investigation common and useful type of sampling related to community medicine are:

1. Simple Random Sampling:

In this method of sampling a sample of, say, ‘n’ units out of N units; S selected such that all the units in the population have an equal chance or probability of being included in the sample.

For the purpose of selection, all the N units in the population are arranged in some unbiased order and are serially numbered.

2. Systematic Random Sampling:

In this method of sampling the 1st unit of the sample is selected at random and the subsequent units are selected in a systematic way as the name itself indicates.

If there are N units in the population and ‘n’ units are to be selected and if ‘r’ is the quotient after dividing N and ‘n’, then one number is selected at random out of the remainder after division and the other units got subsequently by the addition of the quotient ‘r’ to the previous number. This ‘r’ is known as sampling interval.

3. Multistage Sampling:

Here sampling are selected at various stages e.g. prevalence of disease to be estimated in a district. So, test a sample of PHC to be selected at random in first stage, then, at second stage, village is selected at random and in third stage, house is selected from the houses of village.

4. Stratified Random Sampling:

When the population is heterogeneously distributed with regard to characteristics under study. These sub-groups are not equally constituted in the population. In this method of sampling the entire population is divided into certain sub-groups depending upon the characteristics to be studied and simple random sample is drawn independently from each sub-group.

These sub-groups are known as strata:

1. Tables of X²– distribution.

2. Tables of t-distribution.

3. Tables of normal distribution.

4. Gross Reproduction Rate:

It indicates the average number of girls that would be born to a group of women beginning life together. If none died or migrated before reaching the upper limit of childbearing age.

5. Net Reproduction Rate:

This rate indicates the average number of girls that would be produced by women throughout their reproductive period of life if they were exposed at each age to the fertility and mortality rates on which the calculation is based. An allowance is thus made for mortality. A net reproduction rate of 1 indicates that, on the basis of the current fertility and female mortality. The present female generation is exactly maintaining it-self.

6. Child-Woman Ratio:

The child-woman ratio is also known as fertility ratio. It is the number of children 0-4 years of age per 1,000 women of child bearing age, usually defined as women 15-44 years of age. This ratio is used where birth registration statistics either do not exist or are inadequate. It is estimated through data derived from censuses.

7. The Pregnancy Rate:

Pregnancy rate = Number of pregnancies x 100/Exposure in years

8. Marriage Rate:

(i) Crude marriage rate = Number of marriage in the year x 100/Mid-year total population

(ii) General marriage rate = Number of marriage x 1,000 within one year/Number of unmarried person aged 15-49 years

D. Estimation of Population:

1. Increase Method:

= Census Population + (Births – Deaths) + (Immigrants – Emigrants)

2. Arithmetic Progression Method:

P₂ = P₂-P₁/n x d

N = number of years

D = years

3. Geometric Progression Method: