Gene Mapping by Three-Point Test Cross | Cell Biology

In this article we will discuss about:- 1. Introduction to Gene Mapping by Three-Point Test Cross 2. Linkage Mapping Construction 3. Distance and Unit 4. Function.

Introduction to Gene Mapping by Three-Point Test Cross:

Recombination frequencies are directly pro­portional to distances between genes in question and these values can be used in preparation of linkage maps. A three-point test cross (involving three genes) gives us information regarding rela­tive distances between the genes and tells us the linear order in which these genes are present on the chromosome.

An important feature of all linkage maps is their linearity i.e., all genes in a given linkage group can be shown to map in a linear array. Let us presume that there are three genes A, B and C present on the same chromosome (i.e., they are linked).

There could be three possible linear orders in which these genes may be present on a chromosome. These are A-B-C, A-C-B or B-A-C. In one case, B is in the middle and in the other two, C and A respectively are in the middle.

Therefore, in finding out the linear order, the gene present in the centre should be found out.

For this purpose, a three point test- cross is made, which involves crossing of a tri-hybrid ABC/abc (obtained from a cross ABC/ABC X abc/abc) with triple homozygous recessive abc/abc. The progeny obtained will represent the gametes formed by the hybrid. Presuming A-B-C as the order of genes, the results expected can be diagrammatically represented as in the given Fig. 8.16.

Hypothetical frequencies of eight types of progenies are listed in the Fig. 8.17 and can be used for preparation of linkage map.

Linkage Gene Mapping Construction:

Linkage maps are prepared with the help of recombination frequencies.

Let us consider an example from maize involving three endosperm characters. These three characters are coloured aleurone (C) versus colourless aleurone (c), full endosperm (Sh) ver­sus shrunken endosperm (sh) and non-waxy endosperm (Wx) versus waxy endosperm (wx). The data presented by C.B. Hutchinson in 1922 are given in Fig. 8.18.

The three recombination values, i.e., C-Sh, Sh-Wx, C-Wx should be worked out in order to find out the linear order of the three genes, C, Sh and Wx. In the data presented, the progeny of parental types are present in higher frequencies.

C and sh are present together in P₁, therefore, the progeny showing their separation would be recorded as recombination between C and Sh. Similarly recombination between sh and Wx as well as between C and Wx could be recorded.

Gene Order:

The mathematical relationship among the recombination values of three genes may be utilized for determining the gene order. From the values of X, Y and Z of the example (Fig. 8.17), the order of genes can be worked out:

if Z = X -I- Y, the order of genes is A-B-C;

if Z = X – Y, the order of genes is A-C-B;

if Z = Y – X, the order of genes is B-A-C.

In the example (Fig. 8-18), the recombina­tion value C-Wx (21.7%) is nearly equal to recombination value of (C-sh) + (sh – Wx) = 3.5 + 18.4 = 21.9%. Therefore, sh should be located between C and Wx. Another way of determining gene order is comparison of the allelic combination of paren­tal and double crossover recombinant classes of progeny.

Out of the eight (4 pairs) phenotypic classes of progeny, one pair has the highest fre­quency representing parental (non-recombinant) class; and one pair has the lowest frequency representing double crossover recombinant class.

In the example (Fig. 8.18), the highest frequency progeny class develops from non- recombinant gametes, C sh Wx and c Sh wx; and the lowest frequency progeny class develops from double crossover recombinant gametes, C Sh Wx and c sh wx.

Comparison of allelic arrangements of non-recombinant gametes with double crossover recombinant gametes [(C sh Wx and C Sh Wx) or (c Sh wx and c sh wx)] shows that Sh or sh stands out as the changed locus indicating its position in the middle. Therefore, the gene order will be C-sh-Wx.

Gene Mapping Distance and Unit:

The map distance is given by recombination frequency, represented in map unit (m.u.), also called centi-Morgan (cM).

1% recombination = 1 m.u. = 1 cM.

In case of the above example (Fig. 8.18), the linkage map will thus look like the following:

Linkage map may be prepared by another calculation when the gene order is detected directly from the data by comparing the allelic combinations of parental and the double cross­over recombinant classes of progeny. In the example of Fig. 8.18, the gene order determined is C-sh-Wx.

In three-point test cross, some parental com­binations are resulted from double crossovers (products of some multiple crossovers are not recombinant). These crossovers could not be included to determine recombinant frequency between terminal genes. Thus all the map distances based on recombinant frequency might be underestimated of physical map distances.

When the two loci are farther apart on a chromosome, double crossovers occur between them will tend to mask the recombinants. So the distantly linked loci usually appear closer than they really are. Thus more accurate map dis­tances are those established on very closely linked loci.

Therefore, summed short distances are more accurate than directly measured long distances. In the example (Fig. 18.8), the difference between the summed short distance values (3.5 + 18.4 = 21.9) and longer distance value (21.7) is 21.9 – 21.7 = 0.2, which is due to the fact that in the longer distance value double crossovers are not included.

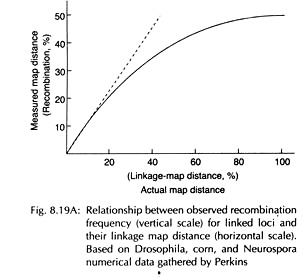
Thus over long distances on a map, the mea­sured map distance (recombination frequency) and actual map distance do not correspond and the linear relationship between the two does not hold good. The recombination frequency between any two genes will never exceed 50, but the map distance may exceed 50.

At lower values there is linear relationship, but as recom­bination value approaches towards 50%, the linear relationship is gradually lost and the recombination frequency is always less than the map distance. This is due to presence of greater number of double and even numbered multiple crossovers which tend to mask recombinants.

Gene Mapping Function:

Actual map distances should not be con­fused with measured map distance based on recombination frequencies. Recombination frequencies need a mathematical treatment (correc­tion) to get relatively precise estimates of map distance between loci. True map distance will actually be obtained by making use of a mapping function as worked out by Haldane (1919).

It reflects the relationship between the real map distance and recombination frequency (RF) which assumes the form of a curve (Fig. 8.19A), showing anticipated increased map distances for longer recombination frequencies. An accurate measure of physical distance is the mean number (m) of crossovers that occur in that segment per meiosis.

Thus the mapping function approach is to find a function that relates RF to ‘m’. In any chromosomal region the various crossover possi­bilities are 0, 1, 2, 3, 4 or more. Any number of crossover produces a frequency of 50% recom­binants (Fig. 8.19B). Thus the only class which is crucial is zero class.

Hence the true determinant of RF is the relative sizes of the classes with no crossovers, versus the classes with any non-zero number of crossovers.

The occurrence of crossovers along a chro­mosome which is responsible for recombination can be described by a statistical distribution called the Poisson distribution, used for events having low mean value. Over a small region of a chromosome, crossing over will take place in a small number of ceils out of the total number of cells undergoing meiosis. If we know the mean value (m) of crossovers in this small region of

M =mean number of crossovers,

I = actual number of crossovers.

For example, if there is an average of one physical crossover event for a particular interval, some cells may have no crossover for that inter­val, whereas others, have one, two, three, etc.

The frequency of cells to have no crossover for that interval may be calculated using Poisson distribution:

Therefore, frequency of cells with at least one crossover in that region in the total popu­lation (i.e., 1.0) will be:

1 – e^-m = 1 – 0.37 = 0.63. These cells will have 50% products recom­binants, so the recombination frequency, RF = ½(1 – e^-m) = ½ X 0.63 = 0.315. Thus a linkage interval of one physical crossover event will show only 31.5% recombinant products whereas 50% recombination would have been expected.

If RF is known, m can be calculated:

RF = ½(1 – e^-m), or, 2RF = 1 – e^-m,

or, e^-m= 1 – 2RF, or, -m = log_n(1 – 2RF),

where log_n = natural logarithm,

or, m = -log_n(1 – 2RF) = Mapping function.

For example, if in a test cross RF is 27.5%, then e^-m = 1 – 2 X 0.275 = 0.45; using calculator we can deduce m = 0.8, i.e. there are 0.8 crossovers per meiosis in that chromosomal region.

The final step is to convert this measure of physical map distance to corrected map unit. In very small genetic regions, RF is expected to be an accurate measure of physical distance because there are not any multiple crossovers. In fact, meiosis will show either no crossovers or one crossover.

The frequency of crossovers (m) will then be translatable into a correct recombinant fraction of ^m/₂ because the recombinants will be ¹/₂ of the chromatids arising from the single crossover class. This defines a general relation­ship between ‘m’ and a corrected recombinant fraction, can be thought of as ^m/₂.

Hence, in the example above, ‘m’ value of 0.8 can be conver­ted into a corrected recombinant fraction of ^0.8/₂=0.4(40%) or 40 map units, which is sub­stantially larger than 27.5 m.u. deduced from observed RF.

The ‘m’ value or actual average number of crossovers will be an index of true map distance in a region (m = 1 =50 cM, m = 2 = 100 cM, m = 3 = 150 cM, m = 4 = 200 cM). ‘m’ value derived through the use of mapping function when plotted against RF values, RF values up to 10% will be linear with map units, but for higher values, the relationship does not hold good, e.g., for RF = 27.5%, m = 0.8 = 40 m.u. = 40 cM.

So if RF values are used for mapping directly without employing mapping function, the distance will be underestimated.