ADVERTISEMENTS:
In this article we will discuss about Arithmetic Mean:- 1. Meaning of Arithmetic Mean 2. Short Cut Method of Determining Arithmetic Mean 3. Merits 4. Demerits.
Meaning of Arithmetic Mean:
The mean is a measurement of unit most frequently used to describe a frequency distribution of same type. The arithmetic mean or average is calculated by dividing the sum (total) of all the individual values of data series by the total number of items.
Example:
ADVERTISEMENTS:
The heights of 10 plants are found to be 15,21,17,19,21,16,14,17,15 and 13 cm. Calculated the arithmetic mean of the plant height.
Solution:
So the arithmetic mean of the plant height is 16.8 cm or the average plant height is 16.8 cm.
ADVERTISEMENTS:
In case of a large number of observations, i.e., more than 10 the arithmetic mean can be calculated by preparing a frequency distribution table. Frequency is the number of individuals representing a class.
1. When the data are discrete and unclassified but tabulated, the arithmetic mean can be calculated in the following way:
Example:
The seed yield (in gms) per plant for 30 maize plants was found to be 110,115,112,108,110,120,115, 112, 108, 115, 121, 115, 110, 112, 108, 121, 110, 110, 115, 112, 110, 115, 112, 112, 115, 110, 112 and 110. Calculate the average yield per plant from the given data.
Solution:
From the given data it is clear that there are some figures which appear more than once, for example seed yield 110g/plant has been recorded in nine plants. So the frequency of plants with 110 g. seed yield in this case is 9.
The frequencies of other values can also be calculated in the same way and the data can be tabulated as follows:
So the average yield per plant is 112.66 gms.
II. When the data of continuous series are classified, then only the frequency of individuals falling in the particular class appears. In such cases for calculation the arithmetic mean, the mid value of each class is taken into consideration and the subsequent steps of computation are like those of discontinuous series.
Example 1: Calculate the arithmetic mean from the following data:
Example 2: Calculate the arithmetic mean of flowers per plant from the following data:
So the average number of flowers per plant is 27.5 or 28.
Short Cut Method of Determining Arithmetic Mean:
ADVERTISEMENTS:
Arithmetic mean can be calculated by short cut method in the following way:
(i) The value of any item in a data series is taken as assumed mean (A). That value may or may not be necessarily present in the series. Generally the item whose frequency is highest is taken as assumed mean.
(ii) From value of each item of the series is now subtracted the value of assumed mean, which gives deviation (dx = X- A). The deviation values are recorded along with their positive or negative sign.
(iii) The deviation value of each item is multiplied with its respective frequency (i.e., dxf) and the sum of all the products (∑ dxf) is determined,
ADVERTISEMENTS:
(iv) The sum of all the products (∑dxf) is divided by the number of items and the value so obtained is added to assumed mean which gives arithmetic mean.
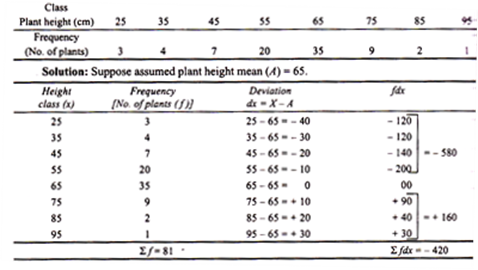
In case the data are classified, the mid-value of each class is considered to calculate the deviation But if the data are not classified and non-tabulated, the following formula is used to calculate the arithmetic mean
Example:
The heights of tomato plants are presented in the following table. Calculate the average plant height by short cut method:
So the arithmetic mean of plant height is 38.65 cm.
Merits of Arithmetic Mean:
1. It is a mathematical mean.
2. It is easy to calculate.
3. It is always definite.
4. It establishes a simple relation among the values of data series.
Demerits of Arithmetic Mean:
ADVERTISEMENTS:
1. It cannot be determined by simple visual observation of data.
2. It cannot be presented by chart or graph.
3. It is not suitable for qualitative studies.
4. Sometimes it does not show representation of series.