ADVERTISEMENTS:
In this article, we propose to discuss about the phyllotaxy (arrangement of leaves).
The mode of arrangement of leaves are of two types. They are: (1) Cyclic Phyllotaxy and (2) Spiral or Alternate or Acyclic Phyllotaxy.
Phyllotaxy is the mode of arrangement of leaves on the stem. It is surprising how regular and strictly mathematical this is. There is a definite law according to which the leaves are arranged on the stem of a particular species. The arrangement is always regular and leaves are never placed on the stem in a haphazard manner.
ADVERTISEMENTS:
The foliage leaves are usually spread about on the stem with long or short internodes between them. This arrangement is called cauline. In some cases, however, the leaves arise as a cluster or a rosette from the very short stem just oh the top of the root.
This arrangement is called radical although the leaves do not actually arise from the root but from a very much condensed stem as in the case of radish.
In cauline leaves there may be one, two, three or more leaves at each node. When there is only one leaf the arrangement is spiral or alternate or a cyclic. This is by far the commonest type of phyllotaxy. When there are two or more leaves at each node the phyllotaxy is cyclic.
A. Cyclic Phyllotaxy:
In the cyclic type of phyllotaxy the leaves at each node form a whorl with the leaves placed on a circle in which the angles between adjacent leaves are the same.
ADVERTISEMENTS:
Thus, if there be two leaves in a whorl, the two will be placed opposite (i.e., at an angular distance of two right angles) one another. If there be three leaves, the angle between leaves in the same whorl is 120° (i.e., one third of a circle), if four, it is 90° and so on.
When there are more than two leaves in a whorl the phyllotaxy is called verticillate.
(A) Opposite Phyllotaxy:
In opposite phyllotaxy the two leaves at each node are always opposite one another. If the successive pairs of leaves be placed at right angles to one another, the arrangement is termed opposite decussate .
In this case, when looked from the top, all the leaves will be found to be arranged along four vertical rows. This is found in Calotropis, Gardenia, Ixora, etc.
In some other plants it is found that the successive pairs are placed exactly on top of one another so that all the leaves lie in one plane and when viewed from above all the leaves are found to lie in two vertical rows.
This type of phyllotaxy is known as opposite superposed . It should be noted that while the superposed type is found in many plants like Psidium guyava (guava), Quisqualis, etc., in many instances the phyllotaxy is initially decussate which later becomes superposed by the flattening out of the twig.
(B) Verticillate Phyllotaxy:
Nerium odorum shows three leaves forming a whorl at each node while Alstonia scholaris shows five or more leaves. These are instances of the verticillate type. Sometimes verticillate phyllotaxy is designated as whorled phyllotaxy.
B. Spiral or Alternate or Acyclic Phyllotaxy:
This is the commonest type of phyllotaxy and the mathematical regularity of the arrangement is astonishing. One can easily verify that (1) the angular distance (angular divergence) between any two consecutive leaves is constant; (2) when looked from the top, all the leaves are found to lie in a fixed number of vertical rows or orthostichies; (3) the orthostichies are evenly dispersed on a circle, the angle between adjacent orthostichies being constant; (4) although leaves look scattered, a close examination shows that leaves are evenly dispersed on all sides of the stem.
To correctly understand the plan of a spiral phyllotaxy one has to imagine a line touching the bases of successive leaves. It will be found that this line forms a spiral (hence the name spiral phyllotaxy) on the stem. This spiral is called the genetic spiral .
This genetic spiral can easily be projected on a flat surface to form a fiat spiral and the position of the leaves may be marked on this spiral. The angle subtended at the centre by two consecutive leaves is the angular divergence. In practice, the angular divergence may be denoted by finding out a leaf which is exactly above a particular leaf, then by counting the number of complete circles covered by the genetic spiral and the number of leaves beginning from the first to the one just before the last. The latter number of leaves -also gives the number of orthostichies. Thus,
Sometimes, only the above fraction is given without calculating the actual divergence in degrees.
ADVERTISEMENTS:
A few instances will clarify the issue:
(1) Distichous or ½ Phyllotaxy:
In the family Gramineae (e.g., Cynodon, rice) the leaf on the second node is just opposite the leaf on the first node, the third leaf is above the first leaf, the fourth above the second and so on (Figs. 156A & 157A). Thus, the angular divergence is clearly 180° (straight angle) and all the leaves fall in two opposite orthostichies (hence, the name distichous). The genetic spiral covers only one circle and there are two leaves on the way in coming to the leaf exactly above the first leaf.
Hence, the angular divergence = ![]() of 360º = 180º. As only the fraction is usually given, the phyllotaxy is also called ½ phyllotaxy.
of 360º = 180º. As only the fraction is usually given, the phyllotaxy is also called ½ phyllotaxy.
(2) Tristichous or 1/3 Phyllotaxy:
In the common sedge (Cyperus rotundus) the leaves are three-ranked (three orthostichies); the fourth leaf is above the first leaf, fifth above second, sixth above third and so on. Three leaves lie in one circle of the genetic spiral. Hence, angular divergence = 1/8 of 360° = 120° or 1/8 phyllotaxy.
(3) Pentastichous or 2/5 Phyllotaxy:
In many common plants like the china-rose and banyan, the 6th leaf is found above the 1st leaf, 7th above the 2nd and so on. The genetic spiral completes two circles in passing these five leaves or five orthostichies . Hence, angular divergence = 2/5 of 360° = 144° or 2/5 phyllotaxy.
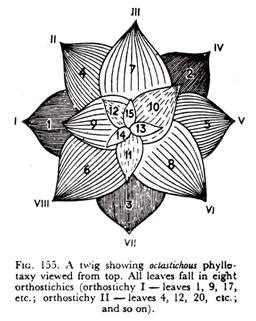
(4) Octastichous or 3/8 Phyllotaxy:
In this case the ninth leaf is found above the first leaf and the genetic spiral completes three circles in this distance as in the case of the papaw (Carica papaya). Thus, there are eight orthostichies . The angular divergence is f of 360° = 135º.
It is rather interesting to note that in the common types of phyllotaxy the fractions of angular divergence lie in a series in which the numerator and the denominator in each
case are obtained by adding up the numerators and denominators of the two preceding phyllotaxies. Thus,
This series is called the fibonacci series or the Schimper-Brown series of divergence.
ADVERTISEMENTS:
When the divergence becomes a big fraction it is not possible to count the orthostichies.
In plants showing these phyllotaxies, usually the internodes are very short so that the leaves are much crowded together. On date and other palms with persistent leaf bases showing such complex phyllotaxy one very close spiral of leaf bases is observed.
This type of phyllotaxy is called parastichous . The sporophylls on a pine cone are also arranged in the same way and the parastichous arrangement can be seen clearly when the cone is viewed from above .
Besides the fibonacci series, which is by far the commonest, there are possibly some other series of phyllotaxy. Two such rare series 1/4, 1/5, 2/8, 3/14…. and 1/2, 2/8, 2/5, 5/8, 8/18…The laws of phyllotaxy may sometimes be disturbed by some torsion of the stem or by incomplete development as towards the apex of a twig.