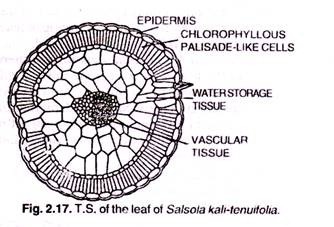
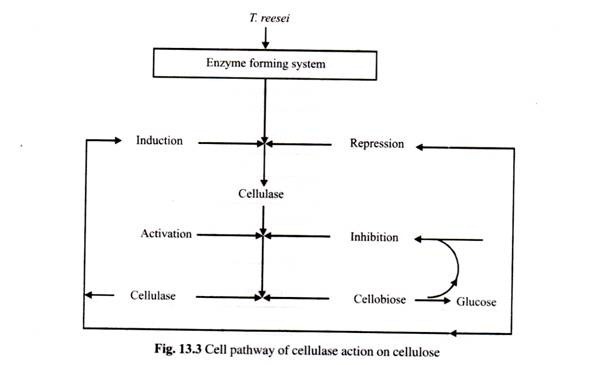
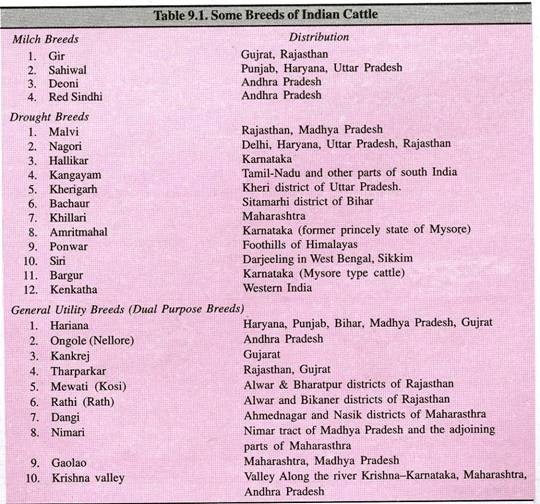
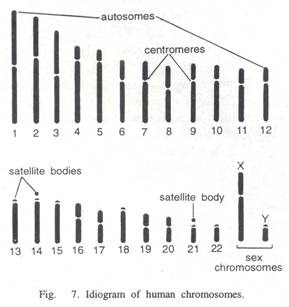
ADVERTISEMENTS:
Read this article to learn about the variation of species and habitats in the ecology and its measurement.
Introduction:
Great variation is observed in the natural world and our earth holds an immense variety of habitats and ecosystem. These habitats and ecosystems shelter a vast group of living organisms in the form of innumerable number of species.
All of this variation in species and habitats is referred to as bio-diversity. Bio-diversity is related to the numbers and relative abundance of species within a community.
ADVERTISEMENTS:
A biological community has an attribute which is called species diversity (Krebs, 1989). The concept of species diversity in community ecology has been intensely debated by ecologists over the years. In fact, Hurlbert (1971) went so far as to suggest that diversity was probably best described as a “mono-concept” because of the many semantic, conceptual, and technical problems associated with its use.
In spite of debates and numerous cautionary remarks put forth by many regarding their use, biological species diversity has remained very popular with ecologists. The most obvious measure of species diversity is the number of species of some taxonomic groups in an area. Number of species is not the only way of looking at diversity, however, the abundance of each species can also be taken into consideration.
The importance of considering the relative abundance as well as number of species can be illustrated by two hypothetical “communities” both containing 10 same species and 100 individuals. Although both communities consist of 10 same species, the relative abundance may be different. Suppose, in community one, 90% of the individuals belong to a single species and the remaining 10% are distributed among the nine other species.
On the other hand, in community two, ten species each accounted for 10% of the total number of individuals. In the first case the evenness of species distribution is considered low, whereas it is maximum in the second case. It is hoped that a distribution will be found fitting the data from many different types of communities and allowing the comparison of different communities through the parameters determining the two distributions. Some of these distributions were proposed as purely empirical fits to the data.
ADVERTISEMENTS:
Others, however, were derived from hypotheses about how the abundance of the species in the community should be related to each other. It had been hoped that, by specifying a set of conditions and deriving the distribution resulting from these hypotheses, specific conclusions about the interactions and relationships between the species and their environment could be tested.
This approach has not been very fruitful, because the same distribution can often be derived from contrasting sets of initial premises. In addition, two distributions derived from conflicting postulates can sometimes both adequately fit an observed set of data. The situation is analogous to the problem of fitting mathematical distributions to the observed spatial dispersion pattern of a species.
Therefore, even if the hypothesized distribution does fit the observed species abundance relationship data, the fit neither proves nor disproves the postulates of the model. However, in terms of purely subjective value, the -use of these models can help to summarize an observed species abundance relationship, and to create heuristic hypothesis about interactions among the species in a community.
Because of the impossibility of determining the numbers of all the species in an area, species diversity studies are invariably carried out on collection of particular taxonomic groups, such as the soil arthropods in 1 square meter of soil or the planktons in 1 cubic meter of water-body. A community is necessarily arbitrarily limited both to area and taxonomy. Commonness is also a relative factor.
A deer population of five individuals per acre is common, but a bacterial species with 100,000 individuals per acre is quite rare. The effect of relative commonness can seriously bias measures of species diversity if disparate taxonomic groups are both included in the group of species taken to be the community. For example, it is difficult to make meaningful comparisons between deer and bacteria purely on the basis of their abundances. In this article only species diversity measurement is discussed.
However, interested reader may consult the following references for species-area relationships and species-abundance relationships. Species-area relationships can be measured by following Preston method (Preston, 1962) and species- abundance relationship can be assessed through geometric distribution (niche preemption hypothesis), broken-stick distribution, and lognormal distribution (Whittaker, 1972; May, 1981; Giller, 1984 ; see also Poole, 1974 and Ludwig and Reynolds, 1984).
Species diversity may be thought of as being composed of two components. The first is the number of species in the community, which ecologists often refer to as species richness. The second component is species evenness or equitability. Evenness refers to how the species abundances are distributed among the species.
Over the years, a number of indices have been proposed for characterizing species richness and evenness. Such indices are termed as richness indices and evenness indices. Indices that attempt to combine both richness and evenness into a single value are referred to as diversity (heterogeneity) indices. In the following sections different types of indices and the procedures for computing of these are described.
Species Richness:
Some communities are simple enough to permit a complete count of the number of species present, and this is the oldest and the simplest concept of species diversity – the number of species in the community. Margalef (1958) coined the name species richness to describe this concept. Complete counts can often be done in some communities, such as in bird communities in small habitat. But it is often impossible to enumerate every species in most of the communities. The larger the sample, the greater the expected number of species. The following procedures have been used to measure different species richness indices.
ADVERTISEMENTS:
Jackknife Index:
This estimate is based on the observed frequency of unique species in the community and is obtained as follows (Helteshe and Forrester, 1983). A unique species is defined as a species that occurs in one and only one quadrat. Unique species are spatially rare species and are not necessarily numerically rare, since they could be highly aggregated. From Heltshe and Forrester (1983),
The Jackknife estimate of the number of species is as under:
where (S) = Jackknife estimate of species richness
ADVERTISEMENTS:
s = observed total number of species present in n quadrats
n = total number of quadrats sampled
k = number of unique species
ADVERTISEMENTS:
The variance of this Jackknife estimate of species richness is given below:
Where var (S) = Variance of Jackknife estimate of species richness
Fj = number of quadrats containing j unique species (j = 1, 2, 3, …… ,s)
ADVERTISEMENTS:
k = number of unique species
n = total number of quadrats sampled
This Variance can be Used to Obtain Confidence Limits for the Jackknife Estimator as follows:
This index tends to overestimate the number of species in a community (Heltshe and Forrester, 1983). This bias is usually less than the negative bias of the observed number of species (5), which, as a rule, is always less than the true value of species richness in the community. Jackknife estimator of species richness is twice the observed number of species. So, this approach cannot be used for communities with exceptionally large numbers of unique species or communities that have been sampled too little (so that S is low).
Bootstrap Procedure:
This is an alternative method of estimating species richness from quadrat samples (Smith and van Belle, 1984). This method is related to the Jackknife, but it requires simulation on a computer to obtain estimates.
ADVERTISEMENTS:
The Essence of the Bootstrap Procedure is as follows:
1. Draw a random sample of size n from the q quadrats within the computer, using sampling with replacement; this is the “bootstrap sample”.
2. Calculate the estimate of species richness from the equation (Smith and van Belle, 1984) below:
Where B(S) = Bootstrap estimate of species of richness
5 = observed number of species in original data
ADVERTISEMENTS:
Pi = proportion of the n bootstrap quadrats that have species i present
3. Repeat steps 1 and 2 N times in the computer, where N is between 50 and 200.
The variance of this bootstrap estimate is given below:
where var [B(S)] Variance of the bootstrap estimate of species richness
n, pi, pj = as defined above
qij = proportion of the n bootstrap quadrats that have both species i and species j absent
According to Smith and van Belle (1984), the Jackknife Index is appropriate when the number of quadrats is small and, in case of large number quadrats, bootstrap is more useful.
Species Heterogeneity or Diversity:
Diversity or heterogeneity indices incorporate both species richness and evenness into a single value.
Whittaker (1972) Defined three Distinct Levels of Diversity of Interest to Ecologists:
(1) Alpha (α) or within habitat diversity;
(2) Beta (β) or between habitat diversity (i.e., changes along environment gradients); and
(3) Gamma (γ) or large scale landscape diversity (a composite of α and β diversity). First alpha diversity is dealt in detail and then the β and γ diversity.
The Shannon—Wiener Index (H’):
This index has probably been the most widely used index in community ecology. It is based on information theory (Shannon and Wiener, 1949) and is a measure of the average degree of “uncertainty” in predicting to what species an individual chosen at random from a collection of S species and N individuals will belong.
This average uncertainty increases as the number of species increases and as the distribution of individuals among the species becomes even. Thus, H’ has two properties that have made it a popular measure of species diversity: (1) H’ = 0 if and only if there is one species in the sample, and (2) H’ is maximum only when all S species are represented by the same number of individuals, that is, a perfectly even distribution of abundances.
The equation for Shannon—Wienner function, which uses natural logarithms (In), is as under:
where H’ is the average uncertainty per species in an infinite community made up of S species with known proportional abundances p1, p2, p3, …….. ps. S and pi‘s are population parameters and, in practice,
H’ is estimated from a sample as below:
where niis the number of individuals belonging to the ith of S species in the sample and n is the total number of individuals in the sample. Equation (7) is the most frequent from of this index used by ecologists. However, this estimation is biased because the total number of species in the community (S) will most likely be greater than the number of species observed in the samples (S). Fortunately, if n is large, this bias will be small.
Brillouin Index:
Many community samples would be treated as collections rather than as a random sample from a large biological community (Pielou 1966). In any case in which the data can be assumed to be a finite collection and sampling is done without replacement,
The appropriate information theoretic measure of diversity is Brillouin’s formula:
where H = Brillouin’s index
N = total number of individuals in entire collection
n1 = number of individuals belonging to species 1
n2 = number of individuals belonging to species 2 (etc.)
Margalef (1958) was the first to propose using Brillouin’s index as a measure of divesity.
There is much argument in the literature about whether the Brillouin index or the Shannon-Wiener index is a better measure of species diversity (Peet, 1974 ; Washington, 1984). In practice, this argument is irrelevant to field ecologists. Because H1 and H1 are nearly identical for most ecological samples (when N is large). Legendre and Legendre (1983) also point out that Brillouin’s index cannot be used when biomass, cover, or productivity is used as a measure of species importance in a community. Only the number of individuals can be used in equation (8).
Beta and Gamma Diversities and their Relationships with Alpha Diversity:
Alpha diversity is also known as local diversity; it is the number of species in a small area of more or less uniform habitat. Gamma diversity or regional diversity is the total number of species observed in all habitats within a region. By region, ecologists generally mean a geographic area that includes no significant barriers to dispersal to organisms.
Thus, the boundaries of a region depend on which organisms are considered. The important point is that, within a region, distributions of species should reflect their selection of suitable habitats rather than their inability to disperse to a particular locality (Ricklefs and Miller, 1999).
When each species is found in all habitats within a region, local (α) and regional (γ) diversities are equal. Ecologists refer to the difference in species from one habitat to the next as beta diversity. The greater the difference, or turnover, of species between habitats, the greater will be the beta diversity.
An example can be cited to discuss the relationship between alpha, beta and gamma diversity. Suppose there are four regions and each region containing four habitats. In first case (a) the diversity in each habitat (alpha diversity) is the same of all four habitats (let each habitat contains species A and B, species richness of 2 (average = 8/4 = 2).
The regional diversity (gamma) is also 2 (in the region there is only 2 species). The beta (turnover) diversity is gamma/alpha = 2/2 = 1. In second case (b) out of four habitats, one contains species A and B, next C, next D and last one E. Alpha diversity is 2 for one habitat (species A and B) and 1 for the other three (species C, D, and E occur alone in each habitat, yielding an average alpha diversity ({2 + 1 + 1 + 1}/4) of 1.25. Gamma diversity is 5 (altogether 5 species in all four habitats), so beta diversity is gamma/alpha (5/1.25) = 4.
In third case (c) two habitats contain A species and another two with B species. The alpha diversity is (1 + 1 + 1 + 1)/4 = 1, and in the region there are two species and hence, the gamma diversity is 2, beta diversity is 2/1 = 2. In last case (d), each habitat is occupied with the same three species A, B and C.
Therefore, alpha diversity is 12/4 = 3, in the region there are three species and gamma diversity is 3 and beta is 3/3 = 1. Regions (a) and (d) have same beta diversity but alpha and gamma diversities are different, indicating little species turnover in those areas.
Evenness Measures:
In a sample when all species are equally abundant, it seems intuitive that an evenness index should be maximized and decreased toward zero as the relative abundance of the species diverges away from evenness.
Two Formulations are Possible:
where D = observed index of species diversity
Dmax = maximum possible index of diversity, given S species and N individuals
Dmin = minimum possible index of diversity, given S and N.
These two measures (labeled V’ and V by Hurlbert, 1971) are convergent for large samples, and evenness measures of the first type (V’) are most commonly used in the literature. All evenness measures range from 0 to 1.
For the Shannon-Wiener Function, Maximum Possible Diversity Occurs According to the following formula:
Probably the Most Common Evenness Index used by Ecologists is Based on the Shannon-Weiner Function:
J’ = H’/H’max … (12)
where J’ = evenness measure (range 0 to 1)
H’ = shannon-Weiner function (equation 6)
H’max = maximum value of H (equation 11)
There is general problem with all measures of evenness; all assume that the total number of species in the community is known (Pielou, 1969). But this number is almost always impossible to determine for species rich communities. Since observed species numbers must always be less than true species numbers in the community, the evenness ratios are always overestimated (Sheldon, 1969). Peet (1974, 1975) and Routledge (1983) recommended that evenness measures should not be used in ecological work unless the number of species in the whole community is known. This may be possible in some temperate zone communities and in well-studied tropical communities (Krebs, 1989).
Conclusion:
Species diversity is a dual concept that includes the number of species in the community and the evenness with which the individuals are divided among the species. There are many ways of measuring species diversity and much controversy about which indices of diversity are best.
All Diversity measures have some limitations and this includes species richness indices, diversity indices, and evenness indices. These measures are easy to compute, but are usually difficult to interpret. In some communities with few species it is easy to determine the species richness. But in all other cases, the species list and the sample size are directly proportional.
The rarefaction technique allows one to adjust a series of samples to a common sample size (number of individuals) so that species richness can be compared among samples (Krebs, 1989). Jackknife estimate of species richness can be made for quadrat sampling. Species richness and evenness are confounded by heterogeneity measures in a single index of diversity. Heterogeneity measures place most weight on the rare species in the sample, and the Shannon-Wiener function is an example of these measures.
With the help of the ratio of observed heterogeneity to maximum possible heterogeneity, when all species have the same number of individuals, evenness can be estimated. Evenness measures have not been used to much advantage in community analysis because all measures are biased upward unless the total number of species in the community is known.